Definition of Independent

Def. Independent : events A, B are independent if $ P( A \cap B) = P(A) \times P(B) $

If A and B are events with P(B) > 0, then the conditional probability of A given B: $ P(A|B) = \frac{P(A \cap B)}{P(B)} $

Intuition: $ P(A \cap B) = \frac{3}{10}, P(B) = \frac{5}{10} \to P(A | B) = 0.6, \text{ (5 B and 3 A)} $

A >     11010 00010
B >     11111 00000
C >     01111 11110
P(A)    AA.A. ...A.  0.4
P(B)    BBBBB .....  0.5
P(C)    .CCCC CCCC.  0.8
P(A&B)  OO.O. .....  0.3
P(A|B)  OO.O.        0.6

Independence of events A,B,C,…

events A,B,C are indep. if \(P(A,B)=P(A)P(B), \ P(B,C)=P(B)P(C), \ P(A,C)=P(A)P(C), \ P(A,B,C)=P(A)P(B)P(C)\)

Newton Pepys problem (AD.1693)

下列哪一种出现机会大？

  • A. 掷出 6 个骰子，至少出现一个 6
  • B. 掷出 12 个骰子，至少出现二个 6
  • C. 掷出 18 个骰子，至少出现三个 6
\[P(A) = 1 - (\frac{5}{6})^5 = 0.665 \\ P(B) = 1 - (\frac{5}{6})^{12} - \binom{12}{1} \frac{1}{6} (\frac{5}{6})^{11} = 0.619 \\ P(C) = 1 - \sum_{k=0}^{2} \binom{18}{k} (\frac{1}{6})^k \times (\frac{5}{6})^{18-k} = 0.597\]
k:有几个骰子是六。C 中的sum算式为 binomial probability

Definition of Conditional Probability

Def. : $ P(A|B)= \frac{P(A \cap B)}{P(B)} $, if P(B) > 0.

  • P(A|B) pronouce: “P of A given B”
  • 排除掉 不是B 的區域，排除掉B complement
  • Normalization: 除以 P(B)

Theorem 1 : $ P(A \cap B) = P(B) \times P(A | B) = P(A) \times P(B | A) $ Theorem 2 : $ P(A_1,A_2,…,A_n) = P(A_1) P(A_2 | P_1) \ \times \ P(A_3 | A_1,A_2) \ \times \dots \times \ P(A_n | A_1,A_2,\dots,A_{n-1}) $ Theorem 3 (Bayes's rule) :

$ P(A|B) = \frac{P(B|A) \ P(A)}{P(B)} $

Law of total probability

Let $ A_1,… ,A_n $ be a partition of the sample space S (i.e., the $ A_i $ are disjoint events and their union is S), with $ P(A_i) > 0 $ for all i. Then

\[P(B) = \sum_{i=1}^{n} P(B \cap A_i) = \sum_{i=1}^{n} P(B|A_i) P(A_i)\]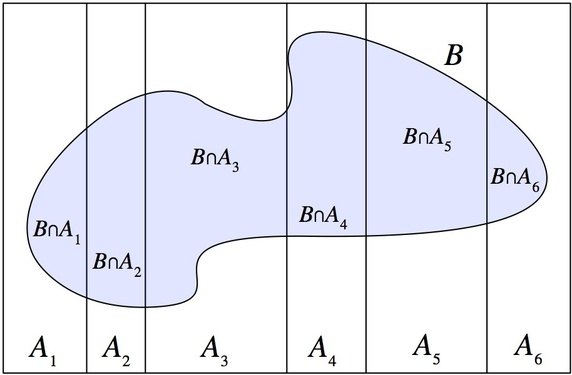

img

Practice

在一副扑克牌中取两张牌，問:

  1. P( 两张都是A 至少一张A ) = ?
  2. P( 两张都是A 有一张是A spade ) = ?

P( 两张都是A | 至少一张A ) = $ \frac{ \binom{4}{2} / \binom{52}{2} }{ 1 - \binom{48}{2} / \binom{52}{2} } = \frac{1}{33} $

P( 两张都是A | 有一张是A spade ) = $ \frac{ \binom{3}{1} / \binom{52}{2} }{ \binom{51}{1} / \binom{52}{2} } = \frac{1}{17} $

Disease Tests

Patients get tested for a disease afflicts 1% of population. Suppose the tests advertised as “95% accurate”. D: patient has disease. T: patient tests positif.

95% accuracy = $ P(T | D) = 95 \% = P(T^c | D^c) $

What is the probability of a test reflects the correct result? P(D | T) = ?

\[P(D|T) = \frac{ P(T|D) \ P(D) }{P(T)} = \frac{ P(T|D) \ P(D) }{ P(T|D) P(D) + P(T|D^c) P(D^c) } \\ = \frac{0.95 \times 0.01}{ 0.95 \times 0.01 + 0.05 * 0.99 } = 16.1 \%\]

整體人口的患病機率小，導致測試準確率在整體人口中變低

举例: 1000人中，10人患病(1%),測試可以準確反映出這10人陽性；另一方面，未患病的990人中，測試錯誤的標出了50人陽性(~5%)。因此測試陽性共有60人，只有10人正確：10/60 = 16.67%

pitfalls & biohazards

  1. cond. independence $ \neq $ independence
  2. Prosecutor’s fallacy: Should ask P(innocence|evidence), NOT P(evidence|innocence)

Monty Hall problem

3 doors

img

Assumptions:

  • 主持人需要打开一扇参赛者没选的门 (Mueser and Granberg 1999).
  • 主持人打开的门后必定是羊，不可为车.
  • 主持人会给参赛者选择，维持原先选择的门的决定，或是换成剩下那扇没开的门.

img

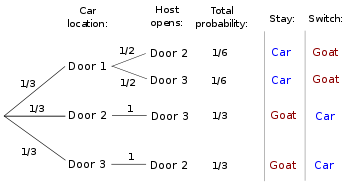
Steps in tree diagram:

  1. contestant choose a door
  2. car behind which door?
  3. host open which door?

What’s the probability of winning a car after “Switch”?

The moment of deciding Switch or not, we already know: Monty open which door

P(win|Monty open door “2”) = ?

\[\frac{1/3}{1/6 + 1/3} = \frac{2}{3}\]

Solution using LOTP

assuming we know where the car is

S : succeeds winning the car (assuming switch) \(D_j\) : Event Door j has car.

\[P(S) = P(S|D_1) \times P(D_1) + P(S|D_2) \times P(D_2) + P(S|D_3) \times P(D_3) \\ = P(S|D_1) \times \frac{1}{3} + P(S|D_2) \times \frac{1}{3} + P(S|D_3) \times \frac{1}{3} \\ = 0 + 1 \times \frac{1}{3} + 1 \times \frac{1}{3} \\ = \frac{2}{3}\]

Simpson’s paradox

两位医生A,B ，A医生每一个手术的成功率都高于医生B，是否代表A所有手术加总的成功率也高于B？ NO 考虑下面的例子：

医生   A             B
手术   心脏  双眼皮   心脏  双眼皮  
成功    70     10      2    81
失败    20      0      8     9
%      78%   100%    20%   90%
% all  80%           83%

Ex.2 : X球员，棒球打击率每一季都高于 Y球员，但三季加总却是Y球员较高。

Ex.3 : ABXY 四个罐子，里头装着 O X 两种糖；A罐中O糖的比率比B罐多，X罐中O糖的比率比Y罐多。混合 A+X 罐, B+Y罐，是否A+X罐的糖比B+Y罐的多？ NO

A            B
o:70 x:20    o: 2 x: 8  0.78 > 0.2

X            Y
o: 9 x: 1    o:80 x:10  0.9  > 0.89
-----------------------------------
A+X          B+Y
o:79 x:21    o:82 x:18  0.79 < 0.82

Gambler’s ruin

两个赌徒，每回合互赌1元。开始时 A 有 i 元, B 有 (N - i) 元。 p = P(A赢某一回合), q = 1 - p. Question: P(A获胜) = ? （B ruined) Random walk:

0         i-2  i-1  i    i+1  i+2  i         N
|----+----+----+----+----+----+----+----+----|

p = P(向右走一步)

“absorbing states”: at 0 & N

Hint: recursive structure, first step analysis

Strategy: conditioning on the 1st step

\[p_i = P( \text{A wins the game} | \text{A starts with i dollars}) \\ p_i = p \times p_{i+1} + q \times p_{i-1}, \text{with}\ 1 \le i \le N-1, \begin{cases} P_0 = 0, \\ P_N = 1 \end{cases} \\ \text{boundary conditions:}\ p_0 = 0, p_N = 1\]

LOTP:

case A wins a certain round and wins the game: \(p \times p_i\)

case A lose a certain round but wins the game: \(q \times p_{i-1}\)

Hints:

this is a difference equation.

Quadratic equation

\[ax^2 + bx + c = 0 \\ x = \frac{-b\pm\sqrt{b^2-4ac}}{2a}\]

L’Hôpital’s rule

\[\lim_{x\to c}\frac{f(x)}{g(x)} = \lim_{x\to c}\frac{f'(x)}{g'(x)}\]

Solution:

First guess: let \(p_i = x^i\)

\[x^i = p \times x^{i+1} + q \times x^{i-1} \\ \to \ 0 = p \times x^{i+1} - x^i + q \times x^{i-1} \\ \to \ 0 = px^2 - x + q \\ x = \frac{1\pm(2p-1)}{2p} \in \{ 1, \frac{q}{p} \} \\ \text{assuming}\ p \neq q \\ p_i = A \times (root_1)^i + B \times (root_2)^i = A1^i + B(\frac{q}{p})^i \\ p_0 = 0 = A + B \implies B = -A \\ p_N = 1 = A1^N + B(\frac{q}{p})^N = A \times (1 - (\frac{q}{p})^N) \implies A = \frac{1}{1 - (\frac{q}{p})^N} \\ p_i = A1^i + B(\frac{q}{p})^i = A \times ( 1 - (\frac{q}{p})^i ) = \color{blue}{ \frac{ 1 - (\frac{q}{p})^i }{ 1 - (\frac{q}{p})^N }, if\ p \neq q } \\ \text{assuming}\ p = q, \\ x = \frac{q}{p} \\ \lim_{x\to 1}\frac{1-x^i}{1-x^N} = \lim_{x\to 1}\frac{\frac{d}{dx}(1-x^i)}{\frac{d}{dx}(1-x^N)} = \lim_{x\to 1}\frac{ix^{i-1}}{Nx^{N-1}} = \color{blue}{\frac{i}{N}, if\ p = q} \\ \\ Solution: \\ \begin{cases} \frac{ 1 - (\frac{q}{p})^i }{ 1 - (\frac{q}{p})^N }, & if\ p \neq q \\ \frac{i}{N}, & if\ p = q \end{cases}\] 
if i=N-i, p=0.49
--- N ---- P(A wins) ---
   20            0.4
  100            0.12
  200            0.02