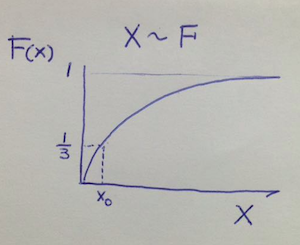问题: 多久可以搜集到所有种类的扭蛋玩具？

问: 有 N 种扭蛋玩具，每次随机获得一件玩具；多久可以搜集到所有种类的玩具？

Find expected time T

\(T_1\) : time until 1st new toy.

\(T_2\) : the addtional time until 2nd new toy.

\(T_3\) : the addtional time until 3rd new toy.

\[T = T_1 + T_2 + T_3 + \cdots + T_N \\ \begin{cases} T_1 & = & \ 1 \\ T_2 - 1 & \sim & \ Geom(\frac{n-1}{n}) \\ T_3 - 1 & \sim & \ Geom(\frac{n-2}{n}) \\ ... & & \\ T_j - 1 & \sim & \ Geom(\frac{n-(j-1)}{n}) \end{cases}\]
* T_x - 1, 减一因为我们使用0开始的 Geom convention。
\[\begin{align} E(T) & = E(T_1) + E(T_2) + E(T_3) + ... + E(T_n) \\ & = 1 + \frac{n}{n-1} + \frac{n}{n-2} + ... + \frac{n}{1} \\ & = n ( 1 + 1/2 + 1/3 + ... + 1/n ) \\ & \approx n \log n \mathsf{\text{ ,for large n}} \end{align}\]

Universality

\[X \sim F \mathsf{\text{, F is CDF of r.v. X}} \\ F(x_0) = \frac{1}{3} \\ \begin{align} P ( F(X) \le \frac{1}{3} ) & = ? \\ & = P ( X \le x_0 ) \\ & = F ( x_0 ) \\ & = \frac{1}{3} \end{align}\]

Logistic distribution