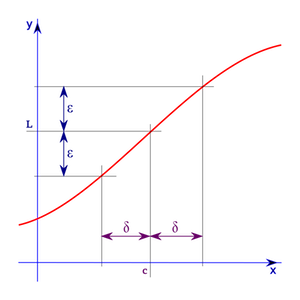
Definition

ε : epsilon 某個很小的數

δ : delta

$ \lim_{x \to c} f(x) = L $ 表示, ∀ ε > 0 則必可以找到對應的 δ > 0

∋ 0 < | x - c | < δ ⇒ | f(x) - L | < ε

當 x 與 c 的距離小於 δ 那麼 f(x) 與 L 的差距就會小於 ε

試證明 : \(\lim_{x \to 2} 3x + 4 = 10\) prove: ∋ 0 < | x - 2 | < δ ⇒ | 3x + 4 - 10 | < ε | 3x + 4 - 10 | = 3 | x - 2 | , 令 δ = ε / 3, 即可保證 0 < | x - 2 | < δ

常見解法:

  • 直接帶入 : 若帶入分母不會為零，則可直接將 x → a 的值帶入
  • 對消 : 將分子與分母 拆解 後對消，獲得分母不為零的狀況，再 [直接帶入]
  • 無限大 : 依據最高次方決定. $ x^x > x! > c^x > x^c > \log x > \sin x $
  • 有理化 : 如 $ \lim_{x \to \infty} \sqrt{x^2 + 6x} - x = ?$

夾擠原理 Squeeze Theorem

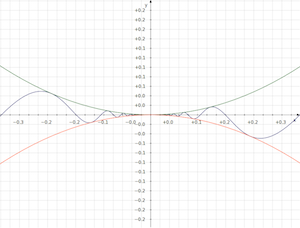
若 h(x) ≤ f(x) ≤ g(x), 而且 $ \lim_{x \to a} h(x) = L, \lim_{x \to a} g(x) = L $ , 則:

\[\lim_{x \to a} f(x) = L\]

單邊極限

若 $ f(x) = \frac{|x|}{x} $, 求極限 $ \lim_{x \to 0} f(x) $

右極限，由右靠近，x 為正數 $ \lim_{x \to 0^+} f(x) = 1 $

左極限，由右靠近，x 為負數 $ \lim_{x \to 0^-} f(x) = -1 $

因為 左極限 不等於 右極限，所以 極限不存在。

極限值若要存在，左極限 必須等於 右極限

\[\lim_{x \to a^+} f(x) = \lim_{x \to a^-} f(x)\]

img